数据结构

数据结构(十)AVL

Posted by YaPi on August 25, 2019

二分搜索树的缺陷

根据添加入树的顺序不同，树可能会退化称为链表，所以需要有一定的机制去避免。

AVL树 (两个俄罗斯人的名字简写)

通常被认为是最早的自平衡的二叉树,二分搜索树的变种

AVL树中定义的平衡二叉树

对于任意一个节点，左子树和右子树的高度差不能超过1(可以左边比右边高，也可以右边比左边高)， 平衡二叉树的高度和节点数量之间的关系也是O(logn)的

平衡因子： 左右子树的高度差

AVL树是对二分搜索树的一种改进，所以它满足二分搜索树的性质，及左边大于右边值，并且，左右两颗子树都是二分搜索树

构建

当插入的这个节点，在插入过后会不平衡的节点的左侧的左侧

右旋转

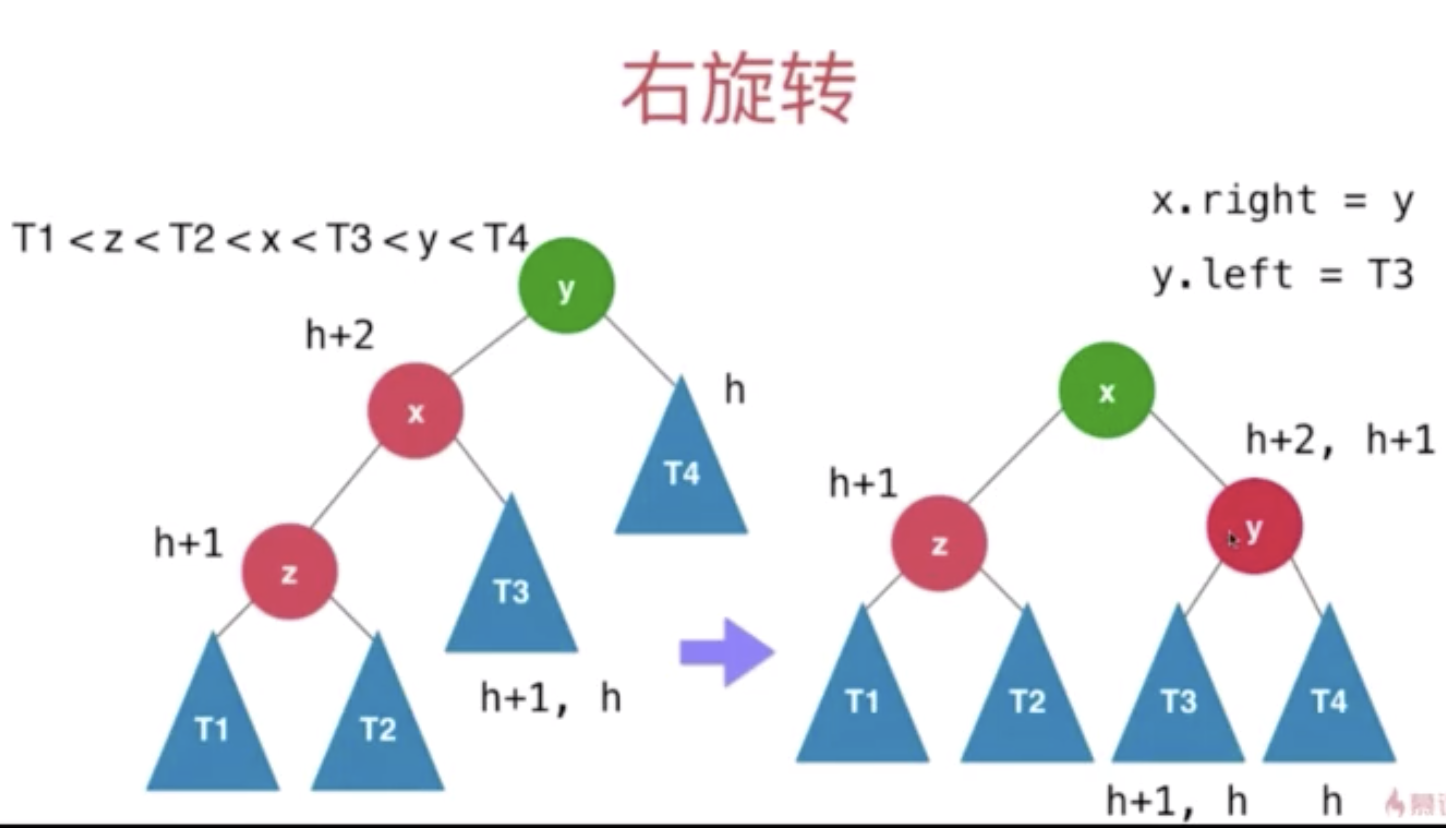
avatar

左旋转

//
//	   y						   x
//	  / \					  	 /   \
//	T1   x    左旋转(y)		 	y     z
//		/ \		--->		   / \   / \
//	   T2   z				  T1 T2 T3  T4
//         / \
//	     T3	  T4
//

实例

/*
@date : 2019/09/17
@author : YaPi
@desc : AVL树 对二分搜索树的一种改进
*/
package tree

import (
	"dtSt/common"
	"dtSt/queue"
	"fmt"
	"math"
)

// 树节点
type AvlNode struct {
	// 值
	value 			common.E
	left,right	*AvlNode
	// 高度(不是树的深度，代表该节点为根节点的子树的高度)
	height		int
	// 节点值
	key 		string
}

func (n AvlNode) CompareTo(e common.E) int {
	return n.value.CompareTo(e)
}

func (n AvlNode) String() string {
	return n.value.String()
}

func newAvlNode(e common.E) *AvlNode {
	return &AvlNode{value: e,height:1}
}

// AVL树
type AVL struct {
	node 	*AvlNode
	size 	int
}

func NewAvl() *AVL {
	return &AVL{}
}

func getHeight(node *AvlNode)int  {
	if node == nil {
		return 0
	}
	return node.height
}

// 获取当前节点的平衡因子
// 在AVL树中，是左子树的高度减去右子树的高度
func getBalanceFactor(node *AvlNode)int  {
	if node == nil {
		return 0
	}
	return getHeight(node.left) - getHeight(node.right)
}

func avlDlr(node *AvlNode)  {
	if node == nil{
		return
	}
	fmt.Println(node.value)
	avlDlr(node.left)
	avlDlr(node.right)
}

func avlLdr(node *AvlNode,keys []common.E)  {
	if node == nil{
		return
	}
	avlLdr(node.left,keys)
	fmt.Println(node.value)
	keys = append(keys, node.value)
	avlLdr(node.right,keys)
}

func avlLrd(node *AvlNode)  {
	if node == nil{
		return
	}
	avlLrd(node.left)
	avlLrd(node.right)
	fmt.Println(node.value)
}

func avlContains(node *AvlNode, d common.E)bool{
	if node == nil {
		return false
	}
	r := node.value.CompareTo(d)
	if r == -1{
		return avlContains(node.right,d)
	}else if r == 1{
		// 当前节点的值比它大，那么需要在左子树中去查
		return avlContains(node.left,d)
	}else{
		return true
	}
}

func avlAdd(node *AvlNode,d common.E)(*AvlNode,bool){
	isAdd := false
	// 将nil当作一个为NULL的子节点,那么,判断当程序找到下一个节点是
	// NULL的时候，则代表需要新加一个节点
	if node == nil {
		return newAvlNode(d),true
	}
	// 若b不为空的时候，则继续向下判断
	// 说明当前节点大于需要新增的节点
	res := node.value.CompareTo(d)
	if res == 1{
		node.left,isAdd = avlAdd(node.left,d)
	}else if res == -1{
		node.right,isAdd = avlAdd(node.right,d)
	}else{
		// 相等 不做操作
	}
	balanceFactor := getBalanceFactor(node)
	// 当前这个节点添加节点过后，需要重新计算高度
	if isAdd {
		bHeight := getHeight(node.right)
		lHeight := getHeight(node.left)
		if bHeight >= lHeight {
			node.height = bHeight + 1
		}else {
			node.height = lHeight + 1
		}

		// 计算平衡因子
		if math.Abs(float64(balanceFactor)) > 1{
			fmt.Println("unbalanced")

			// LL
			if balanceFactor > 1 && getBalanceFactor(node.left) >= 0{
				return rightRotate(node),true
			}
			// RR
			if balanceFactor < -1 && getBalanceFactor(node.right) <= 0{
				return leftRotate(node),true
			}
			// LR
			if balanceFactor > 1 && getBalanceFactor(node.left) < 0 {
				node.left = leftRotate(node.left)
				return rightRotate(node),true
			}
			// RL
			if balanceFactor < -1 && getBalanceFactor(node.right) > 0 {
				node.right = rightRotate(node.right)
				return leftRotate(node),true
			}
		}
	}

	return node,isAdd
}
// LL
//			y						 x
//		   / \					   /   \
//		  x   T4    右旋转(y)	  z   	y
//		 / \		--->		 / \   / \
//	    z   T3					T1 T2 T3  T4
//     / \
//	  T1  T2
//
func rightRotate(y *AvlNode)*AvlNode {
	x := y.left
	t3 := x.right
	x.right = y
	y.left = t3

	// 更新节点的height值
	// 只需要更新x和y的值，并且需要先更新y的值
	y.height = 1 + int(math.Max(float64(getHeight(y.left)),float64(getHeight(y.right))))
	x.height = 1 + int(math.Max(float64(getHeight(x.left)),float64(getHeight(x.right))))

	return x
}


// RR
//	   y						   x
//	  / \					  	 /   \
//	T1   x    左旋转(y)		 	y     z
//		/ \		--->		   / \   / \
//	   T2   z				  T1 T2 T3  T4
//         / \
//	     T3	  T4
//
func leftRotate(y *AvlNode)*AvlNode {
	x := y.right
	t2 := x.left
	x.left = y
	y.right = t2

	// 更新节点的height值
	// 只需要更新x和y的值，并且需要先更新y的值
	y.height = 1 + int(math.Max(float64(getHeight(y.left)),float64(getHeight(y.right))))
	x.height = 1 + int(math.Max(float64(getHeight(x.left)),float64(getHeight(x.right))))

	return x
}


func avlRemoveMind(node *AvlNode)*AvlNode{
	if node.left == nil {
		rNode := node.right
		node.right = nil
		return rNode
	}
	node.left = avlRemoveMind(node.left)
	return node
}

func avlRemoveMax(node *AvlNode)*AvlNode{
	// 若右孩子为空，则当前节点为最大节点
	if node.right == nil {
		// 找到最大节点，找到其左孩子，左孩子为删除掉当前节点后的最大节点
		lNode := node.left
		node.left = nil
		return lNode
	}
	node.right = avlRemoveMax(node.right)
	return node
}

// 找二分搜索树的最小节点
func avlMind(n *AvlNode)*AvlNode{
	if n.left == nil{
		return n
	}
	// 获取节点的最右节点
	//lNode := mind(n.left)
	//if lNode != nil{
	//	return lNode
	//}else {
	//	return n
	//}
	return avlMind(n.left)
}

// 找二分搜索树的最大节点
func avlMax(n *AvlNode)*AvlNode  {
	// 若当前节点为空 返回nil
	if n.right == nil{
		return n
	}
	// 获取节点的最右节点
	return avlMax(n.right)
}

// 删除任意节点
func avlRemoveElement(node *AvlNode,e common.E)*AvlNode{
	// 非空判断
	if node == nil{
		return nil
	}
	// 和当前节点的值进行比较
	switch node.CompareTo(e) {
	case 1:
		// 当前节点的值比需要删除的值大
		// 需要在当前节点的左孩子进行查找
		node.left = avlRemoveElement(node.left,e)
	case -1:
		// 当前节点的值比需要删除的值小
		// 需要在当前节点的右孩子进行查找
		node.right = avlRemoveElement(node.right,e)
	case 0:
		// 需要删除的值就是当前值
		// 若当前节点没有左孩子和右孩子
		if node.left == nil && node.right == nil{
			node = nil
		}else if node.right != nil && node.left == nil {
			// 若当前节点只有右孩子 没有左孩子
			// 需要找到右子树当中最小的元素 用最小的元素当作当前节点的值
			n := avlMind(node.right)
			// 删除最小的元素 并返回删除过后的树
			// rNode := avlRemoveMind(node.right)
			rNode := avlRemoveElement(node.right,n.value)
			n.right = rNode
			node = n
		}else if node.left !=nil && node.right == nil {
			// 若当前节点只有左孩子 没有右孩子
			// 找到左子树当中最大的元素 用最大的元素当作当前节点值
			n := avlMax(node.left)
			// lNode := avlRemoveMax(node.left)
			lNode := avlRemoveElement(node.left,n.value)
			n.left = lNode
			node = n
		}else if node.left != nil && node.right != nil {
			// 当前节点既有左孩子 也有右孩子
			// 找到左子树最小的值 作为当前节点的值
			n := avlMind(node.right)
			// avlRemoveMind 没有维护自平衡，所以直接复用当前方法
			//rNode := avlRemoveMind(node.right)
			rNode := avlRemoveElement(node.right,n.value)
			n.left = node.left
			n.right = rNode
			node = n
		}
	default:
	}

	if node == nil {
		return nil
	}
	// 判断是否需要维护node节点的平衡性
	balanceFactor := getBalanceFactor(node)


	node.height = 1 + int(math.Max(float64(getHeight(node.right)),float64(getHeight(node.left))))

	// 计算平衡因子
	if math.Abs(float64(balanceFactor)) > 1{
		fmt.Println("unbalanced")
		// LL
		if balanceFactor > 1 && getBalanceFactor(node.left) >= 0{
			return rightRotate(node)
		}
		// RR
		if balanceFactor < -1 && getBalanceFactor(node.right) <= 0{
			return leftRotate(node)
		}
		// LR
		if balanceFactor > 1 && getBalanceFactor(node.left) < 0 {
			node.left = leftRotate(node.left)
			return rightRotate(node)
		}
		// RL
		if balanceFactor < -1 && getBalanceFactor(node.right) > 0 {
			node.right = rightRotate(node.right)
			return leftRotate(node)
		}
	}

	return node
}

// 判断是否是一颗平衡二叉树
func isBalanced(node *AvlNode)bool  {
	if node == nil{
		return true
	}
	balanceFactor := getBalanceFactor(node)

	if math.Abs(float64(balanceFactor)) > 1{
		return false
	}
	return isBalanced(node.left) && isBalanced(node.right)
}

// 判断是否是一颗平衡二叉树
func (b *AVL)IsBalanced()bool  {
	return isBalanced(b.node)
}

func (b *AVL)RemoveElement(e common.E)  {
	n := avlRemoveElement(b.node,e)
	if n!= nil{
		b.size --
	}
}

func (b *AVL)RemoveMind()  {
	b.node = avlRemoveMind(b.node)

}

func (b *AVL)RemoveMax()  {
	b.node = avlRemoveMax(b.node)
}


func (b *AVL)Max()*AvlNode  {
	return avlMax(b.node)
}

func (b *AVL)Mind()*AvlNode  {
	return avlMind(b.node)
}

// 层序遍历(又叫广度优先遍历) 借助队列
func (b *AVL)LevelOrder()(l []AvlNode){
	// 借助队列实现
	q := queue.NewArrayQueue()
	node := b.node
	q.Enqueue(b.node)
	for !q.IsEmpty() {
		node = q.Dequeue().(*AvlNode)
		// 将节点添加到数组里面返回
		l= append(l, *node)
		if node.left != nil {
			q.Enqueue(node.left)
		}
		if node.right != nil{
			q.Enqueue(node.right)
		}
	}
	return
}


// 二分搜索树前序遍历
func (b *AVL)DLR(){
	// 先遍历当前节点
	// 再遍历左子树
	// 再遍历右子树
	avlDlr(b.node)
}

// 二分搜索树中序遍历
func (b *AVL)LDR(keys []common.E){
	// 先遍历当前节点
	// 再遍历左子树
	// 再遍历右子树
	avlLdr(b.node,keys)
}

// 二分搜索树后序遍历
func (b *AVL)LRD(){
	// 先遍历当前节点
	// 再遍历左子树
	// 再遍历右子树
	avlLrd(b.node)
}


func (b *AVL) Add(d common.E) {
	rNode,ok := avlAdd(b.node,d)
	b.node = rNode
	if ok {
		b.size ++
	}
}

func (b *AVL) Size() int {
	return b.size
}

func (b *AVL) IsEmpty() bool {
	return b.size == 0
}

func (b *AVL) Remove(d common.E) {
	avlRemoveElement(b.node,d)
}

func (b *AVL) Contains(d common.E) bool {
	return avlContains(b.node,d)
}
FEATURED TAGS
JVM docker Kubernetes mongodb redis mysql golang 设计模式 Python SpringBoot 大数据 数据结构 SpringCloud 运维 架构师 typeScript Go微服务 go C++ Rust Vue3 Shell
FRIENDS