2-3树
满足二分搜索树的基本性质,但是它不是一种二叉树,它有两种节点,节点可以存放一个元素或这两个元素,存放一个元素时有左右两个孩子,存在两个元素的节点有三个孩子
2-3树添加节点不会添加到一个null的位置,比如从头开始添加节点,添加c,而后添加b的时候不会成为c的孩子节点。而会成为c的左孩子,当继续添加d的时候还是会添加到b旁边,成为3个节点,然后,从b进行分裂,d,c成为他的子孩子。
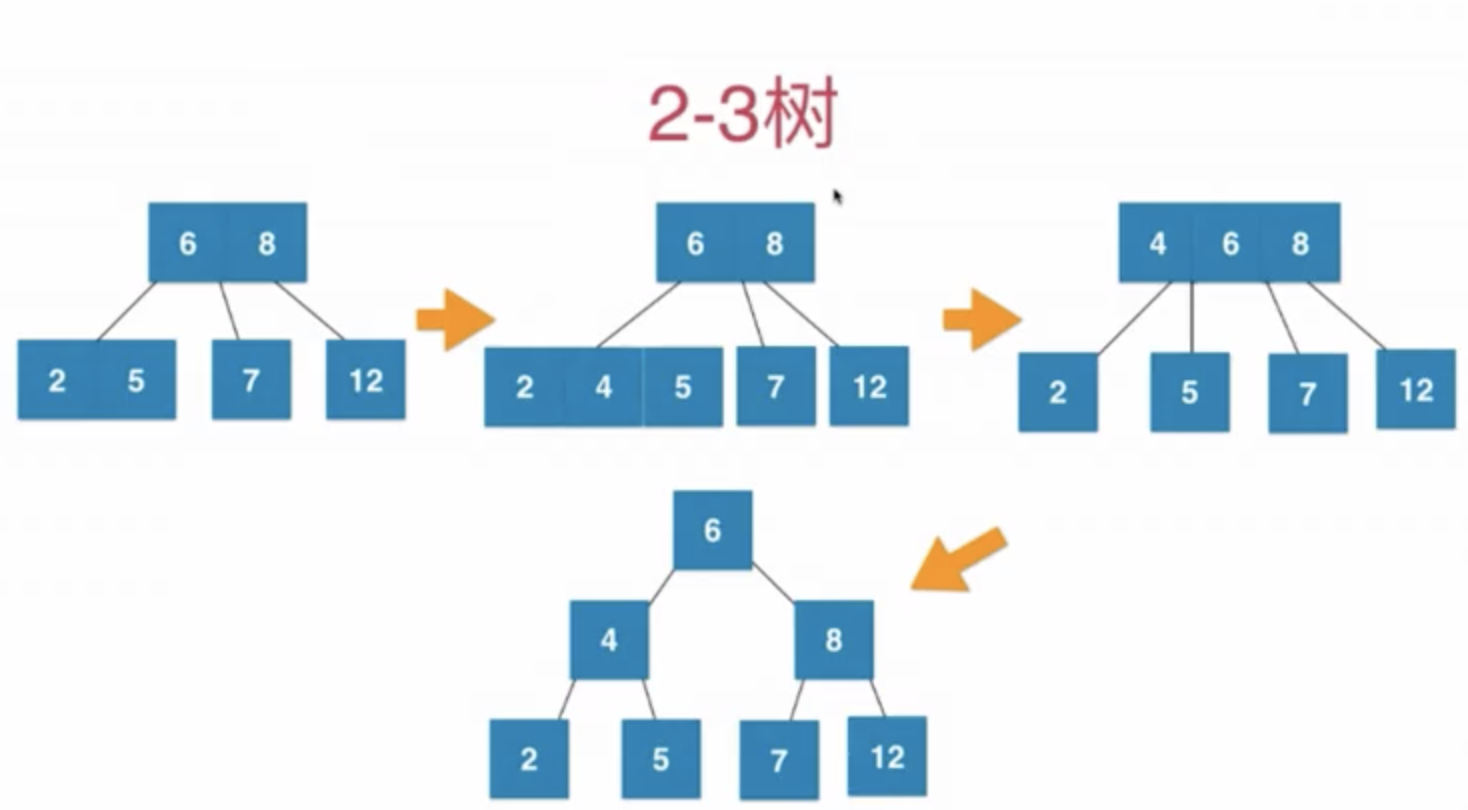
2-3树
b c
/ | \
a1 a2 a3
a1 < b < a2 < c < a3
2-3树是一颗绝对平衡的树(从根节点到叶子节点经过的节点数量是相同的,左右子树的高度是一致的)
红黑树与2-3树之间的关系
红黑树当中黑色的节点,和2-3树中的2节点相同 红黑树中用一个黑色节点连接一个红色节点来代表一个三节点。所以,一个红色节点表示:它和它的父节点一起表示一个2-3树中的一个三节点,并且红色节点一定是向左倾斜的
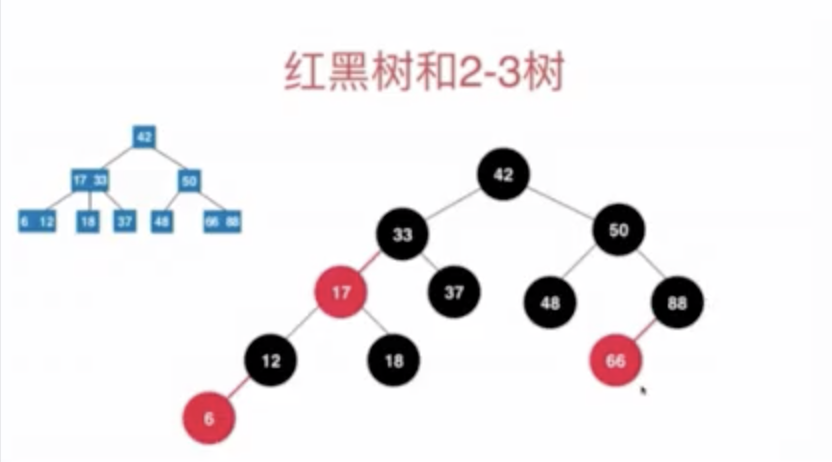
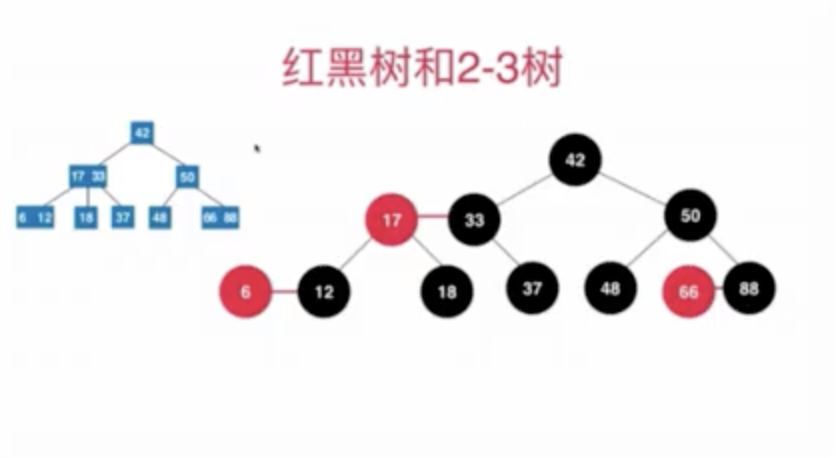
红黑树定义
- 依然是二分搜索树
- 每个节点或者是红色或是黑色
- 根节点是黑色
根节点要么是2节点,要么是3节点,不管是2节点还是3节点,它的颜色都是黑色的
- 每一个叶子节点(不是我们以前认为的叶子,而是最后的空节点)是黑色的
- 如果一个节点是红色的,那么他的孩子节点都是黑色的
不管它的子节点是2节点还是3节点,它的根节点都是黑色的
- 从任意一个节点到叶子节点,经过的黑色节点是一样的
2-3树是一颗绝对平衡的树,从2-3的任意一个节点到叶子节点所经过的点数是一样的,当从红黑树的任意一个节点到叶子节点时,都会走过相同的黑色节点。一般就说红黑树是保持黑平衡的二叉树(黑色节点保持着绝对平衡)
- 如果一个节点是黑色节点,如果有有孩子那么他的右孩子一定是黑色的
红黑树三节点添加
红黑树和AVL树的比较
红黑树的高度是 2logN,所以在查询上面的性能会比AVL树性能低一点,但是在红黑树中添加和删除的时候会比AVL树快速一点。所以对于经常发生改变的数据用红黑树,对于创建了就不变了,多用于查询的数据,最好用AVL树存储。
性能总结
对于完全随机的数据,普通的二分搜索树就很好,因为不会退化成链表
对于查询较多的使用情况,AVL树很好用
对红黑树来说,它牺牲了平衡型,它不是一个平衡二叉树,但是它的统计性更优(综合增删查改所有的操作)